Baby Steps
You don’t have to see the whole staircase, just take the first step—Martin Luther King, Jr.
|
| Still from her IHES lecture |
Maryna Viazovska was the first person to prove an exact bound on sphere packing in a dimension higher than 3. She achieved this for dimension 8 in 2016 by making an improvement of 0.00001 over one previous paper by Henry Cohn and Noam Elkies. This also led to the solution in dimension 24, joint with Cohn and Abhinav Kumar, Stephen Miller, and Danylo Radchenko.
Today we talk about partial progress—baby steps—and its relation to solving conjectures.
This post is a continuation of our recent thoughts about how those who claim to have solved a major problem almost always claim to have solved the whole thing in one large leap. We’ve thought about declaring a rule that any claim on a major open problem, at least about complexity lower bounds, must first be a partial result. We will give concrete suggestions in that direction at the end. But on reflection, we’ll curb the dogmatics a little.
In her 2016 Quanta article on Viazovska’s breakthrough, Erica Klarreich quotes Peter Sarnak:
“It’s stunningly simple, as all great things are. You just start reading the paper and you know this is correct.”
We hasten to add that the paper’s correctness is evident amid the context that others had established over the previous two decades, going back at least to Thomas Hales’s voluminous proof of Johannes Kepler’s conjecture for dimension 3. To quote Klarreich:
Researchers have known for more than a decade what the missing ingredient in the proof [of optimality for dimensions 8 and 24] should be—an “auxiliary” function that can calculate the largest allowable sphere density—but they couldn’t find the right function. … [F]inding the right modular form allowed Viazovska to prove [the case of 8] in a mere 23 pages.
Thus Viazovska brought in a new tool to the problem, modular forms, which had already proved their merit in resolving the Fermat conjecture. But she still needed to choose the right modular form among many candidates. Klarreich quotes her as saying it is difficult even just to explain how she knew which one to use. This brings us back to the challenge of explaining—or debunking—the flash of insight that claimers claim to have. At least in this case, per Sarnak’s quote, the proof was in the pudding.
|
| From Cohn’s 2017 AMS Notices article |
To complete the mixing of our original message, the examples we chose happen to involve improvements by tiny amounts. We’ve even understated Viazovska’s above: reckoned against a later paper by Cohn and Elkies, her improvement was
The recent post where we discussed the phrase “the proof is in the pudding” involves a number with six more 
Steps Toward Matrix Multiplication
We have covered other work on the exponent 
In 2005, however, Cohn wrote a paper with Robert Kleinberg, Balazs Szegedy, and Christopher Umans on ideas for taking 
The objective need not be 
Other recent work by Alman and Williams shows both a dimension along which the road down to
Some Partial Progress Objectives
Cohn also has a page of informal thoughts on how to perform research, including advice for those who claim to have solved some open problem. We want to add this advice:
Make sure ahead of time that your advance really covers the intermediate ground it jumps through. Even better, walk back your claim a little so that it proves something only a step or so beyond previous knowledge.
|
| source (not this) |
Here are a few examples of such things to prove in complexity theory:
-
: The claim is that SAT requires exponential time.
-
A Baby Step: Prove SAT cannot be done in linear time. Or that it cannot be done in
time.
-
Circuit Lower Bounds: The claim is that some concrete problem in
requires super-polynomial size general circuits.
-
A Baby Step: Prove that some concrete problem cannot be done in a linear size boolean circuit–or one of size
.
-
Factoring: The claim is that factoring a general number
requires super-polynomial time in the bit-length of
- A Baby Step: Prove that factoring cannot be done in linear time. Or not in quadratic time. See this.
- Graph Isomorphism: The claim is that there is polynomial-time algorithm to tell whether two graphs are isomorphic.
- A Baby Step: Prove the case where the graphs have degree a fixed constant.
This is an example of a baby step that is already done. Note: it was not an easy step. It is a famous result of Eugene Luks—see his 1982 paper.
We could go deeper into known computational complexity issues to find more. The idea applies to problems from mathematics in general. Here is one:
-
Riemann Hypothesis” The claim is of course that
only happens for negative even integers and for
with real part
. The latter are the zeroes in the critical strip where the real part is between
. The sum is convergent for real part
and its analytic continuation for other
- A Baby Step: Prove that it is impossible for just two zeroes to be off the half line. Or that only a finite number can be off the half line.
We invite readers to add more favorite math examples in comments, or others from complexity theory.
Open Problems
What are some additional first steps?
Have we also—unintendedly but effectively—made a case for the value of tiny improvements? At least when they are conceptual improvements?
Here is the answer to the puzzle in the previous post: Barbara wins. She forces the sum of every row to be 
[inserted “in dimension 8” at top, added note on “analytic continuation” for Riemann, other tweaks]
Well, for separating VP from VNP, partial progress has been made. Limaye, Srinivasan, Tavenas recently proved superpolynomial lower bounds Against low-depth algebraic circuits.
This is super-interesting, as using chasm at depth 3/4, one can get strong lower bounds against general circuits assuming strong enough lower bounds against depth 3/4 circuits. Taking a series of baby steps may ultimately lead to the resolution of the general problem.
Re: You don’t have to see the whole staircase, just take the first step.
— Martin Luther King, Jr.
Plato’s Puppet Returns
Between the discovery and the invention,
Falls the Shadow, who knows, you know,
By tracking backward, retracing the steps
Of the tourist, who comes not to conquer,
But to enjoy the winding stair to the place.
— Also Sprach 0*
I have made the first step of proving that the Robin inequality is true for all n>5040 which are not divisible by any prime number between 2 and 953, where we all know that if the Robin inequality is true for all n>5040, then the Riemann Hypothesis is true.
For several months, I was struggling in the battle of how to move forward on this result. However, this week I found a beautiful proof in which I could extend that result and finally prove that the Robin inequality is true for all n>5040. It’s too soon to celebrate and claim that the Riemann Hypothesis is true. However, this is an interesting puzzle in case you might find for some proof of the Riemann Hypothesis which is almost easy to understand.
For that reason, I leave you to your consideration:
https://www.preprints.org/manuscript/202109.0480/v1
Thanks in advance!!!
Frank, I have to compliment you on an excellent paper. You have proved quite a deal in it. Unfortunately, you have not proven the Riemann Zeta Hypothesis. First let me point out the hole — it is a little subtle and late in the paper — and then I’ll go through what you have proved and a few ideas on how to tighten up your arguments.
In Thm 9.2, your second equation reads $f(n) = f(q_i * m) = f(m) * \frac{q_i^{a_i+2} – 1}{q_i^{a_i+2}-q_i}$. That is incorrect. You used Lemma 8.6 and substituted in $a=a_i$ and $b=1$. If you look carefully at that Lemma, $n$ on the righthand side is $m$ in Thm 9.2, and so you needed to substitute $a=a_i-1$. This causes a number of +1s in the exponents to drop and in particular loses the factor of $N_m$, the $m$th primorial at the bottom of page 17. This invalidates the rest of your argument, as you lose the +1 on the righthand side, and you wind up proving 2 > 1 — not a contradiction.
You have proven that any counterexample to Robin’s inequality must be divisible by all primes =20$ must be divisible by all primes $q < 128$ ($f(n) <= \frac{16513}/{16512} f(2^{13}) f(m) < f(2^{13}mq) < e^\gamma \log\log(2^{13}mq) 5040$.
Then generalize your Lemmas 73-7.5 to the following:
Lemma: Suppose we know that any counterexample to Robin’s inequality greater than 5040 must be divisible by $p^k$ for some prime p >= 3 and k >= 3.
Then any such counterexample must also be divisible by primes q with $q =k$, and p,q not dividing m.
$f(n) = f(p^a) f(2^{20} m) <= p^2/(p^2-1) f(p) f(2^{20} m) <= (q+1)/q f(p) f(2^{20} m) = f(2^{20} pmq)$. Now the argument on the right-hand-side must satisfy Robin's inequality since it is not divisible by $p^k$ and it is larger than 5040.
So $f(n) < e^\gamma \log\log (2^{20} pmq) <= e^\gamma \log\log (2^{20} p^a m) = e^\gamma \log\log n$. Contradiction.
This first lemma with your Lemma 3.5 lets you immediately go from a factor of $2^{20}$ to a factor of $2^20 3^{13} 5^8 7^7 31^4$, and the second fills in all the other primes up to 953.
Argh, formatting issues. I was saying that you have proven that any counterexample is divisible by all primes less than or equal to 953.
I was also saying that you can simplify most of your paper considerably with two lemmas.
First, use the fact that f(2^a) = 20 to show that any counterexample has to be divisible by all primes less than 128. (The proof is above, $q$ is a prime less than 128, it follows the pattern of your Lemmas 7.3, 7.4 and 7.5.)
Then simplify 7.3-7.5 into a single lemma as given above.
Take 3: From lemma 8.6 f(2^a) is less than or equal to 16513 over 16512 times f(2^13) when a is greater than 20. Using that fact and 2^13 > 5040, you can follow the logic of your other lemmas to show that any counterexample must be divsible by primes less than 128.
Thank you very much Craig Helfgott. Your help was crucial to improve my paper. I focused in fixing the flaw that you detected and I will study your shortcuts later and add them in new versions. The issue that you detected can be fixed in this way:
f(n \times N_{m}) = f(q_{i}^{2} \times m’) = f(m’) \times \frac{q_{i}^{a_{i} + 2} – 1}{q_{i}^{a_{i} + 2} – q_{i}}
where m’ = \frac{n}{q_{i}} and N_{m} is the primorial number of order m. In addition, we know that f(n \times N_{m}) > f(n). In this way, the other parts of the proof remain the same since
f(n \times N_{m}) – f(m’) > f(n) – f(m’) \geq e^{\gamma} \times \log\log n – f(m’)
and
f(n \times N_{m}) – f(m’) &= f(m’) \times \frac{q_{i}^{a_{i} + 2} – 1}{q_{i}^{a_{i} + 2} – q_{i}} – f(m’)
I added you to the Acknowledgments section of the paper for your cooperation:
https://zenodo.org/record/5545868
I wish you the best!!!
It’s not too simple to fix it. It’s actually this result:
f(n \times N_{m}) = f(q_{i}^{2} \times m’) > f(m’) \times \frac{q_{i}^{a_{i} + 2} – 1}{q_{i}^{a_{i} + 2} – q_{i}}
with a > instead of =
I will still working on this and the approach that you sent me to make shorter the proof.
Thanks.
Now, I fixed using the correct following formula:
f(n \times N_{m}) = f(q_{i}^{2} \times m’) = f(m’) \times \frac{q_{i}^{a_{i} + 2} – 1}{q_{i}^{a_{i} + 2} – q_{i}^{2}}
Note that I used b = 2 correctly this time. It was a very interesting puzzle to solve and I tried to do it today. It’s too soon to celebrate again because a simple new and flawed detail would break the whole proof, but I share it so you could see it by yourself:
https://zenodo.org/record/5545990
Thank you Craig!!!
I have been working in another approach:
https://doi.org/10.5281/zenodo.5532834
The older version won’t work as you explained. This is a very short new version and thus, it would be easy to check it. The reasons why the paper is too short is because it is based on the Vojak’s work which has more than 10 pages (https://arxiv.org/abs/2005.09307). I checked Vojak’s proof and it seems correct.
Thanks for all!!!
But what about baby steps as a consequence of new tools being discovered by outsiders, you cannot make much progress with microscope if you were using only a hammer before. It means that if you approach someone competent with newly just invented microscope they may find no value in it. And, so, your baby steps will be in vain, because your succes is not well understood by people who use hammers.
I don’t think that’s my hypothesis. My function is defined differently for $s$ with real part less than $1$.
Ah, right. Added a note about that. We’ve previously propagated the canard that substituting
gives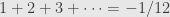 
.
A couple of nice examples you could have chosen along these lines are approximation factors for graphic TSP and now metric TSP.
Sometimes, taking seemingly baby steps may push you to solve the general problem. Take derandomization for Polynomial Identity Testing for example. For the class of polynomials of individual degree s, and number of variables n, we know explicit hitting sets of size (s+1)^n (Trivial hitting set). If you know the polynomials are computable arithmetic circuits of size s, and if you give an explicit hitting set of size (s+1)^n-1 (saving one point from the trivial hitting set), then you derandomize general PIT for arithmetic circuits.
This is from a beautiful recent paper Derandomization from Algebraic Hardness by Guo, Kumar, Saptharishi, Solomon (inspired by earlier work on PIT bootstrapping by Agrawal, Ghosh, Saxena and Kumar, Saptharishi, Tengse and earlier works by Kabanets-Impagliazzo and Agrawal-Vinay).
For the Riemann hypothesis, I propose that a baby step be showing that 50% of the zeros lie on the line. I think the best partial result so far is about 41% by Bui, Conrey, and Young (arXiv:1002.4127).
While it is true that evolution is lot more common than revolution, there are few scenarios where these baby steps become meaningless.
Consider the baby steps of releasing an actual movie or drama. Who would be interested in watching the rehearsals or whatever might be going on behind the scenes?
Hello Craig,
I’m sharing a link with a new attempt:
https://doi.org/10.5281/zenodo.5532834
in case you might wish to share and check it!!!
This is a very short paper and thus, it would be easy to check it. The reasons why the paper is too short is because it is based on the Vojak’s work which has more than 10 pages
(https://arxiv.org/abs/2005.09307). I checked Vojak’s proof and it seems correct.
Thanks for all!!!
It was a giant step.