SAT is Not Too Easy

Lance Fortnow is one of the top complexity theorists in the world, and has proved fundamental results in many aspects of complexity theory. One example, is his famous work on interactive proofs with László Babai and Carsten Lund. More recently, he did a beautiful extension of a result of Boaz Barak on the BPP hierarchy problem, this work is joint work with Rahul Santhanam. Lance is of course famous for the longest running and best blog on complexity theory, and while doing all this he had time to be the founding editor-in-chief of the new ACM journal: Transactions on Computation Theory.

Lance has a great sense of humor and is a terrific speaker. Not too long ago–1997–he gave a talk at an ICLAP without using any visual aids: not chalk, not marking pens, not overheads, not powerpoint, nothing. The talk went well, which says something about his ability to make complex ideas understandable.

Lance has also has played a unique role, I hope he does not mind me saying this, in shaping modern computational complexity. He made a “mistake” in a paper with Mike Sipser that opened a new chapter in complexity theory: this was the discovery that amplification by parallel repetition is not trivial.

In science, especially mathematics, we all try to do correct work, but sometimes the right error can be very important. I would argue that Lance and Mike, by finding that it was not obvious that parallel repetition amplifies, made one of the great discoveries of complexity theory.

An “error” that leads to a great discovery has happened many times before in the history of science. One of the best examples, I think, might be the work of Henri Poincare on the -body problem. Poincare wrote a prize winning paper on solving the -body problem, then discovered that he had made a mistake, and finally discovered what we now call chaos. A pretty good “mistake.” (See George Szpiro’s book for the intriguing story of Poincare’s discovery.)

I have the pleasure to have a joint paper with Lance, and I will talk about that work: various lower bounds on the complexity of SAT. Given that so many believe that SAT is not contained in polynomial time, it seems sad that the best we can prove is miles from that. It is like dreaming that one day you will walk on the moon, but today the best you can do is stand on a chair and look up at it at night. We are so far away.

Perhaps this is a hopeful analogy, since we did eventually walk on the moon. It took many terrific people, some great ideas, a huge effort, and perhaps some luck, but eventually Neil Armstrong and Buzz Aldrin did walk on the moon. Perhaps one day we will show that SAT cannot be computed in polynomial time. Perhaps.

The Results

SAT is of course the problem of determining a truth assignment for a set of clauses, and is the original NP-complete problem. Yet what we know about the complexity of SAT is pretty slim. The conventional wisdom, of course, is that SAT cannot be recognized by any deterministic polynomial time Turing machine. What we believe is vastly different from what we can prove. The best results look like this:

Theorem: No deterministic Turing machine accepts SAT in time and space where

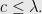
Here is some fixed constant that is unfortunately small: I call it a “”, since the first result was due to Lance.

Initially, it was show by Lance that . Then, it was proved by by Anastasios Viglas and myself that . Note, we made a mistake, but ours was “silly”: for a short time we thought that we could prove . Next Lance and Dieter Van Melkebeek proved that where is the golden ratio, i.e. Ryan Williams has improved this to , which is just above . (Lance points out that the current best of Williams is actually just above .)

The General Structure

In his beautiful paper, Williams, gives a general framework for all the known proofs. If you are interested in working on lower bounds for SAT, you should look at his paper–and ours too. Also check out Iannis Tourlakis’ paper on extensions of these lower bound methods, and Lance’s paper on diagonalization.

Today I want to give you the 50,000 foot view of how such lower bounds are proved. Their general structure is:

1. Assume by way of contradiction some complexity assumption that you wish to show is false;
2. Use this assumption to show that an algorithm exists that speeds up some computation;
3. Finally, show that this speedup is too fast: it violates some known diagonalization theorem.

Williams gives a much lower level description and further formalizes the methods to the point where he can prove negative results, this is a unique aspect of his work. But for today I hope that this summary helps make some sense of the SAT results.

What I find nice about this type of proof is that you get lower bounds by finding new algorithms. The algorithms typically must use some assumed ability, but they are nevertheless algorithms. Donald Knuth asserts that computer science is algorithms, nothing but algorithms. You might find that a bit narrow, but the point is that this lower bound method allows you, no–actually forces you, to think in terms of new algorithms. You do not need to know exotic mathematics, but you must be able to program Turing machines.

Lower bounds proved by this method are strong: the method shows that no Turing machine of a given type can do something. There are usually time and space restrictions on the Turing machines, but no other restrictions. They can do whatever they want within those constraints. Thus, these lower bounds are much stronger than monotone, or bounds of constant depth, or any other bounds that restrict computations in some way.

For the technical expert, I am ignoring the issue of “uniform” vs. “non-uniform”, but I think even an expert will agree that Turing machine lower bounds are very strong. For the non-expert, ignore what I said about ignoring.

The Main Trick

In my view, there is one basic trick that we have used over and over in complexity theory. The trick is one of breaking a problem up into smaller pieces, then solving each of them separately. It is similar to the idea that Savitch used to prove his famous theorem. It is also related to the method used to get a “better” exponential time algorithm for the knapsack problem and for other problems.

Suppose that you want to see if there is a path from to in some graph. Savitch’s trick is to guess a mid-point and check:

The trick that we use to prove these various lower bounds is based on a generalization:

Some like to call the trick the speedup lemma. The point is that if you have some type of nondeterminism you need not check each of these steps, instead you can guess one, and only check that one. By a step I mean for some

Here is another way to think about this idea. Suppose that you need to check the truth of a statement . The statement may be very hard to check, and the obvious way of checking it may be too slow. If you can find a set of statements (sub-problems) so that

then you can check each individual sub-problem separately. The difficulty is that this may still take too much time. However, since space is “re-useable”, for Savitch this works well:

However, we are interested in the time; thus, checking all statements still takes too long,

We need to get the maximum of the time’s to get a “too fast computation.” The trick is then to use nondeterminism, which will allow us to only check one of the statements.

More precisely, we convert into the form:

Then, there is a nondeterministic computation that checks,

by guessing an index and checking the sub-problem . Suppose that the assumption we made allows us to convert a nondeterministic computation into a deterministic one. Then, we have a deterministic computation for , but since it is a deterministic computation, this immediately yields a deterministic computation for which is . This “alternation” technique is the key to how we get speedups.

An important point about this trick. We want , the number of sub-problems, to be as large as possible, since we only have to check one. However, the difficulty with making large is that you need to “write down” in some sense the sub-problems. This tends to force to be small. Roughly, this why the methods get stuck and cannot seem to prove arbitrarily large .

This idea has a long history, it was used by Ravi Kannan in his work on space limited computation. It was also used in the proof of the following famous theorem:

Theorem:

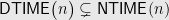
The wonderful result is due to Wolfgang Paul, Nicholas Pippenger, Endre Szemerédi, William Trotter, and will be discussed in a future post. For now note that the conventional wisdom says that much more is true, but this is the best we know: deterministic time is not exactly equal to nondeterministic time.

Open Problems

The obvious goal is to prove at that is true. Even better, prove that . There is strong evidence from Williams that these bounds will require a new idea. He is able to show that in the current framework there is no proof that will even show that is true.

I am generally worried about any “impossibility proof.” By this I mean a proof that says you cannot do something by a certain approach–Williams’ result is of this type. Historically such proofs have been defeated, in other parts of mathematics, by subtle but significant shifts. However, Willaims’ proof does show that it will be impossible, without some new ingredient, to improve the SAT lower bounds. Clearly, we new a new idea.

I must admit I have thought of many ideas, none of which have worked. I will end this post by telling you some of the “dead ends” that I tried, perhaps you can make them work.

• I tried to select many sub-problems, but “name” them in some indirect manner.
• I tried to use PCP technology. This is one of the deepest set of results that we have concerning SAT, but there seems, to me, no way to exploit it.
• I tried to break the computations up in a more arithmetical manner. Can we use the fact that computations can be coded as polynomials to improve SAT lower bounds?

Good luck, I hope you see something that we have missed.